¿Qué es el código binario?
El código binario es un sistema de numeración que utiliza únicamente dos dígitos, 0 y 1, para representar números. 🤓 A diferencia del sistema decimal, que se basa en la numeración del 0 al 9, el sistema binario permite una mayor precisión al trabajar con dispositivos electrónicos. 💻
Cada dígito en el código binario se llama “bit”, y usualmente hay grupos de 8 bits, conocidos como “bytes”. 🤖 Este sistema se utiliza para la representación de datos en dispositivos electrónicos, ya que las computadoras solo pueden entender ceros y unos, verdadero o falso. 🤯
La información que es procesada por la computadora se basa en el código binario y cada operación se realiza en binario. 🔍 Es por ello que el código binario es esencial en el campo de la informática y la electrónica, y su uso es imprescindible en el desarrollo y funcionamiento de estas tecnologías. 🚀
De hecho, el código binario se utiliza no solo en el mundo de los ordenadores, sino también en otros contextos que emplean dos estados diferentes para representar información. Por ejemplo, en el sistema de lectura y escritura táctil conocido como Braille, se utilizan puntos que se ponen en relieve (valor uno) o no (valor cero) para representar los distintos caracteres. 📖
En resumen, el código binario es un sistema fundamental en la informática y la electrónica, y su uso es clave en el procesamiento y almacenamiento de información en dispositivos electrónicos. 🤖👨💻
¿Cómo funciona el código binario?
¡Bienvenidos a una aventura en el funcionamiento del mundo del código binario! 🤖
El código binario es como el ADN de los dispositivos electrónicos. ¡Es la clave para que tu smartphone, tu computadora o tu tablet funcionen! 📱💻📟
Pero, ¿cómo funciona exactamente? Bueno, en el sistema binario solo hay dos dígitos: el 0 y el 1, y cada uno de ellos representa un estado de interruptor, como si estuviera apagado o encendido. ¡Es como si la computadora fuera un gran interruptor con millones de botones! 🤯
Cuando queremos representar un número en binario, convertimos cada dígito en su valor correspondiente de 0 o 1. Por ejemplo, si queremos representar el número 5 en binario, utilizamos los bits 1, 0, 1. ¡Es así de sencillo! 😎
Además, cada conjunto de 8 bits se llama byte, y se utiliza para representar números y caracteres en la computadora. ¡Es como si fueran pequeñas piezas de un rompecabezas que juntas forman un mensaje completo! 🧩
Pero el código binario no es el único sistema de numeración en informática. También existe el sistema hexadecimal y decimal. Y para representar caracteres, existe el código ASCII y UTF-8. ¡Es como un lenguaje secreto para la computadora! 🤫
En resumen, el código binario es esencial para el funcionamiento de la tecnología que utilizamos a diario. ¡Así que la próxima vez que enciendas tu computadora o tu smartphone, recuerda el pequeño mundo de 0 y 1 que lo hace posible! 🌎👨💻
¿Para qué sirve el sistema binario?
El código binario 🧑💻 es el sistema que utilizan los dispositivos electrónicos 📱🖥️ para procesar información. Consiste en una secuencia de ceros y unos que se utilizan para codificar todo tipo de información 📊📈, desde textos 📝 y imágenes 🖼️ hasta sonidos 🔊 y vídeos 🎥. El sistema binario se basa en dos dígitos, 0 y 1, y todo número binario está compuesto por un conjunto de bits 💻, que son las unidades más pequeñas de información. Por ejemplo, cuatro bits forman un número binario, como 1010.
El código binario es utilizado por todas las áreas de la informática y las telecomunicaciones 🌐. Los procesadores actuales hacen uso de este sistema para procesar órdenes y ejecutar tareas 🤖. Además, el código binario se utiliza para cifrar información y realizar transferencia de datos o llevar a cabo comunicaciones entre dispositivos 📡📞.
Este sistema de numeración es muy importante en la informática porque permite codificar y transmitir información de manera eficiente 🚀. Un byte, por ejemplo, es un conjunto de 8 bits que pueden almacenar hasta 256 valores diferentes, lo que permite a las computadoras procesar información de manera más rápida y efectiva.
El código binario tiene una gran cantidad de usos que han permitido que la tecnología avance a pasos agigantados 🚀🚀. Aunque se están trabajando en sistemas aún más complejos, el código binario seguirá siendo de gran utilidad durante muchos años más. ¡Incluso en la antigua China ya se utilizaban conceptos similares al binario en algunas de sus prácticas matemáticas! 🇨🇳
En resumen, el uso del sistema binario es fundamental para la codificación y transmisión de información en la era digital 📡. El código binario es utilizado por los dispositivos digitales en todos los ámbitos, desde la electrónica hasta la informática. ¡Gracias a los ceros y unos, podemos disfrutar de los dispositivos digitales que conocemos hoy en día! 🙌
¿Cómo se traduce el código binario?
El código binario es un sistema numérico que utiliza dos dígitos, representados por ceros y unos 😎. Mientras que los humanos utilizamos el sistema decimal que cuenta con 10 dígitos, las computadoras y otros dispositivos electrónicos utilizan el sistema binario, que solo usa dos dígitos.
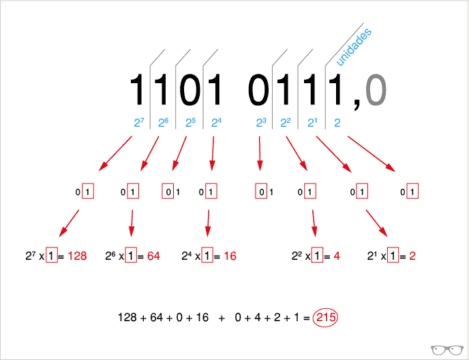
Para traducir un número decimal en un número binario, se divide el número entre 2 y se escribe el resto de la división (0 o 1) en orden inverso al que se obtienen. ¡Es fácil! Por ejemplo, para convertir el número 2019 a binario, dividimos 2019 entre 2, obtenemos 1009 con un resto de 1. Luego, dividimos 1009 entre 2 y obtenemos 504 con un resto de 1. Seguimos dividiendo y escribiendo los restos hasta que el número es igual a cero. El resultado es la representación en binario del número decimal, que en este caso es 111101111111100011 👍.
Del mismo modo, se puede convertir un número binario en su equivalente decimal utilizando una fórmula matemática. Por ejemplo, si tenemos el número binario 1010, lo convertimos en su equivalente decimal mediante la fórmula: (1 x 2^3) + (0 x 2^2) + (1 x 2^1) + (0 x 2^0) = 8 + 0 + 2 + 0 = 10 😃.
El código binario es fundamental para la tecnología digital, ya que permite que las computadoras procesen información de manera eficiente y precisa. Además, es utilizado para la codificación de información, como textos, imágenes, sonidos y mucho más 🤖.
En el caso de que se quiera convertir texto a un sistema binario hay que hacer uso de un traductor binario. Funciona de la misma forma que una calculadora binaria. Basta con escribir las palabras o frases que se quieren traducir y pulsar un pequeño botón 🤓. Por ejemplo, si queremos convertir la palabra “Tecnobits” en sistema binario, el resultado sería “01010100 01100101 01100011 01101110 01101111 01100010 01101001 01110100 01110011” 👏.
En resumen, el sistema binario es un sistema numérico utilizado en la informática y la electrónica que permite la codificación y transmisión de información digital. ¡Así que la próxima vez que uses una computadora o un dispositivo electrónico, recuerda que todos los procesos y transmisiones de datos se basan en el código binario! 😎
Acá de damos algunos ejemplos de como traducir código binario
Ejemplo 1: Para traducir el número binario 101101 a su equivalente decimal, se puede utilizar la fórmula:
1 x 2^5 + 0 x 2^4 + 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 = 45
Por lo tanto, el número binario 101101 es equivalente al número decimal 45.
Como sacamos lo anterior ?
🔢 1. Primero, se escribe el número binario que se quiere convertir. Por ejemplo, el número binario 101101.
🔢 2. Luego, se escriben los exponentes de 2, comenzando por 0 en la posición más a la derecha. En este caso, serían 2^0, 2^1, 2^2, 2^3, 2^4 y 2^5.
🔢 3. A continuación, se multiplican los dígitos del número binario por los exponentes de 2 correspondientes. Para ello, se usa la siguiente fórmula:
(dígito binario) x 2^(exponente de 2)
Por ejemplo, para el primer dígito del número binario 101101, que es 1, se multiplicaría por 2^5, que es el exponente correspondiente a esa posición.
(1) x 2^5 = 32
🔢 4. Se repite el paso anterior para cada dígito del número binario, multiplicándolo por su exponente de 2 correspondiente.
Para el segundo dígito, que es 0:
(0) x 2^4 = 0
Para el tercer dígito, que es 1:
(1) x 2^3 = 8
Para el cuarto dígito, que es 1:
(1) x 2^2 = 4
Para el quinto dígito, que es 0:
(0) x 2^1 = 0
Y para el sexto y último dígito, que es 1:
(1) x 2^0 = 1
🔢 5. Finalmente, se suman todos los resultados obtenidos en el paso anterior:
32 + 0 + 8 + 4 + 0 + 1 = 45
¡Y listo! El número binario 101101 es equivalente al número decimal 45.
Ejemplo 2: Para traducir el número decimal 57 a su equivalente en binario, se puede seguir el siguiente procedimiento:
Dividimos 57 entre 2, obteniendo 28 como cociente y 1 como resto. Dividimos 28 entre 2, obteniendo 14 como cociente y 0 como resto. Dividimos 14 entre 2, obteniendo 7 como cociente y 0 como resto. Dividimos 7 entre 2, obteniendo 3 como cociente y 1 como resto. Dividimos 3 entre 2, obteniendo 1 como cociente y 1 como resto. Dividimos 1 entre 2, obteniendo 0 como cociente y 1 como resto.
Luego, escribimos los restos en orden inverso: 111001. Por lo tanto, el número decimal 57 es equivalente al número binario 111001.
Ejemplo 3: Para traducir la letra “A” a su equivalente en código binario utilizando el código ASCII, se puede consultar una tabla de códigos ASCII.
En esta tabla, la letra “A” tiene un valor decimal de 65. Para convertir este número decimal a binario, se puede seguir el mismo procedimiento utilizado en el ejemplo anterior:
Dividimos 65 entre 2, obteniendo 32 como cociente y 1 como resto. Dividimos 32 entre 2, obteniendo 16 como cociente y 0 como resto. Dividimos 16 entre 2, obteniendo 8 como cociente y 0 como resto. Dividimos 8 entre 2, obteniendo 4 como cociente y 0 como resto. Dividimos 4 entre 2, obteniendo 2 como cociente y 0 como resto. Dividimos 2 entre 2, obteniendo 1 como cociente y 0 como resto. Dividimos 1 entre 2, obteniendo 0 como cociente y 1 como resto.
Luego, escribimos los restos en orden inverso: 1000001. Por lo tanto, la letra “A” en código binario es 1000001.
¿Cómo funciona el código de base 2 o binario ?
👨🏫 ¡Hola a todos! ¿Están listos para aprender sobre el código binario? 🤖
El código binario es una forma de representar información en el sistema electrónico utilizando únicamente dos dígitos: 0 y 1. Cada dígito se llama bit, y se pueden combinar para representar cualquier número o información en el sistema.
🔢 ¿Quieres un ejemplo? Aquí tienes una tabla que muestra los números del 0 al 15 en su forma binaria:
| Número decimal | Número binario |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
🤯 ¡Impresionante, ¿verdad?! Cada número decimal se convierte en una secuencia de 4 bits en su forma binaria, utilizando la potencia de dos para cada bit comenzando por la derecha. El bit más a la derecha equivale a 2 elevado a la 0 (1), el segundo bit a la derecha equivale a 2 elevado a la 1 (2), el tercer bit equivale a 2 elevado a la 2 (4), y el cuarto bit equivale a 2 elevado a la 3 (8). ¡Sumando todos los valores, se obtiene el número decimal original!
Veamos un ejemplo para entender mejor:
Supongamos que tenemos un número binario de cuatro dígitos: 1011. El primer paso es asignar una potencia de dos a cada uno de los dígitos, comenzando por el bit más a la derecha, que equivale a 2 elevado a la 0 (1). El segundo dígito a la derecha equivale a 2 elevado a la 1 (2), el tercer dígito a la derecha equivale a 2 elevado a la 2 (4) y el cuarto dígito a la derecha equivale a 2 elevado a la 3 (8).
| Dígito | Valor en base 2 | Potencia de dos |
|---|---|---|
| 1 | 1 | 2^0=1 |
| 0 | 0 | 2^1=2 |
| 1 | 1 | 2^2=4 |
| 1 | 1 | 2^3=8 |
Luego, se multiplica cada dígito por su respectiva potencia de dos y se suman los resultados. En este caso, la operación sería la siguiente:
(1 x 2^0) + (0 x 2^1) + (1 x 2^2) + (1 x 2^3) = 11
¡Listo! El número binario 1011 es equivalente al número decimal 11.
Este método se puede aplicar para cualquier número binario, independientemente de su longitud. Sin embargo, a medida que aumenta el número de dígitos, el cálculo se vuelve más complejo.
¡Pero esto no es todo! El sistema binario no solo se utiliza para representar números, sino también para codificar información. Por ejemplo, cada letra y símbolo en el alfabeto se asigna a un código binario específico en ASCII (Código Estándar Americano para el Intercambio de Información) y Unicode, lo que permite a las computadoras entender y procesar diferentes idiomas.
🧐 En resumen, el código binario es un sistema fundamental en la electrónica y la informática, ya que permite a las computadoras procesar y almacenar la información. Utiliza únicamente dos dígitos, 0s y 1s, para representar números y datos, y se basa en la asignación de potencias de dos a cada dígito. Así que, ¡ahora sabes cómo funciona el código binario! 😊
¿Cómo pasar código de sistema binario a letras?
🤔 Si te estás iniciando en el mundo de la electrónica y la informática, es normal que sientas que todo es complicado al principio. Pero no te preocupes, aquí te explicaremos de manera sencilla cómo convertir código binario a letras 🙌
Para hacer esta conversión, es necesario conocer el código ASCII. Este código asigna un número binario único a cada letra del alfabeto y otros símbolos comunes. Entonces, para convertir el código binario a letras, se deben agrupar los bits binarios en paquetes de 8, también conocidos como bytes, y luego buscar la letra correspondiente en la tabla ASCII.
Por ejemplo, si tienes el número binario 01100001, debes agrupar los bits en paquetes de 8: 01100001. Luego, consultas la tabla ASCII y encuentras que ese número binario corresponde a la letra “a”. Así de fácil es convertir código binario en letras utilizando el sistema ASCII. 🤓
Es importante destacar que cada byte de código ASCII corresponde a una letra específica y que este sistema de codificación se utiliza en casi todos los sistemas informáticos para representar texto en lenguaje natural. Ahora que sabes cómo se hace, ¡inténtalo tú mismo! Puedes buscar en internet una tabla ASCII para familiarizarte con los códigos de cada letra y símbolo. ¡No te rindas! La electrónica y la informática pueden ser divertidas y emocionantes si se aprende de manera amena y entretenida. 😃
Para convertir código de sistema binario a letras, se deben agrupar los bits binarios en paquetes de 8 y luego buscar la letra correspondiente en la tabla ASCII. Cada conjunto de 8 bits se llama byte y corresponde a una letra específica.
Aquí te dejamos una tabla con algunos ejemplos de cómo se convierte el código binario en letras utilizando la codificación ASCII:
| Código binario | Código ASCII | Letra |
|---|---|---|
| 01000001 | 65 | A |
| 01100010 | 98 | b |
| 01000011 | 67 | C |
| 01100100 | 100 | d |
| 01000101 | 69 | E |
Como puedes ver en la tabla, el código binario se agrupa en bytes de 8 bits, y luego se busca la letra correspondiente en la tabla ASCII utilizando el valor numérico del byte. Por ejemplo, el número binario 01000001 se refiere al valor numérico 65 en el código ASCII, lo que corresponde a la letra “A”.
Esperamos que esta tabla te haya sido útil para entender cómo se convierte el código binario en letras utilizando la codificación ASCII. 😊
¿Cómo es la relación entre código binario y los lenguajes de programación?
La relación entre el código binario y los lenguajes de programación es fundamental. 😎 El código binario es el lenguaje que utiliza la computadora para procesar información, 🤖 y aunque es muy preciso y confiable, resulta difícil de entender y trabajar para los humanos 😅, ya que consta únicamente de una serie de unos y ceros. Por suerte, para facilitar la programación, se han creado los lenguajes de programación. 🚀
Los lenguajes de programación son formas más fáciles y comprensibles de comunicarse con la máquina. 🤓 Estos lenguajes utilizan palabras y símbolos que son más familiares para nosotros, y tienen una sintaxis más cercana a nuestro lenguaje natural. 📝 Los programas escritos en estos lenguajes se traducen a código binario, lo que permite que la computadora pueda entender las instrucciones y llevar a cabo las operaciones necesarias. 💻
Es importante destacar que existen distintos lenguajes de programación, cada uno con sus propias características y finalidades. 💡 Algunos de los lenguajes más populares son Python, Java, C++, JavaScript, entre otros. 🌟
En resumen, el binario es la base para entender cómo la computadora procesa la información, mientras que los lenguajes de programación son una forma más eficiente para comunicarnos con ella. 😊
Y aquí te dejo la tabla con un ejemplo para que puedas entender mejor la relación entre el código binario y los lenguajes de programación:
| Lenguaje de programación | Código binario |
|---|---|
| Python | 01110000 01111001 01110100 01101000 01101111 01101110 |
| Java | 01001010 01100001 01110110 01100001 |
| C++ | 01000011 00101011 00101011 |
| JavaScript | 01001010 01100001 01110110 01100001 01010011 01100011 01110010 01101001 01110000 01110100 |
¡Espero que te haya resultado útil y divertido! 😁
Historia del sistema binario: de Leibniz a los sistemas informáticos
El sistema binario ha sido utilizado desde tiempos muy antiguos. La obra china clásica “I Ching”, escrita alrededor del año 1200 antes de Cristo, fue la primera en mostrar el uso del código binario. Los hexagramas del “I Ching” fueron ordenados de manera similar al código binario que usamos hoy en día. Los egipcios también utilizaron el código binario para la contabilidad en sus jeroglíficos hace unos 2400 años antes de Cristo.
Pero fue un matemático indio llamado Pingala quien usó el primer sistema binario al cien por cien para contar sílabas de poemas. Luego, en el siglo XVII, Gottfried Wilhelm Leibniz, un matemático alemán, desarrolló el sistema binario moderno y pensó en un método para hacer operaciones matemáticas con números binarios. Sin sus cálculos, los ordenadores no existirían tal como los conocemos hoy.
🤔 ¿Cómo es la evolución del sistema binario en la era de los ordenadores?
Hoy en día, el sistema binario se utiliza en los sistemas informáticos como base numérica, ya que es la forma más fácil para que la máquina procese la información. El código binario, que utiliza únicamente 0s y 1s para representar cualquier número o información en un sistema electrónico, es difícil de leer para los humanos. Los lenguajes de programación se desarrollaron para comunicarse con la máquina de una manera más eficiente y comprensible. Los lenguajes de programación se traducen a código binario para que la máquina pueda entender las instrucciones y realizar las operaciones necesarias.